BBO 实用函数
在这个开源 Python 模块中,我们为 BBO 提供了一些常用的实用函数,如下所示。这些函数的主要目的是简化 BBO 的典型开发和实验流程。
绘制二维适应度地形图
- pypop7.benchmarks.utils.generate_xyz(func, x, y, num=200)[源代码]
在绘制适应度地形的二维等高线图之前,生成必要的数据。
- 参数:
func (func) – 基准测试函数。
x (list) – x 轴范围。
y (list) – y 轴范围。
num (int) – x 轴和 y 轴范围内的采样点数量(默认为 200)。
- 返回:
一个 (x, y, z) 元组,其中 x、y 和 z 分别是 x 轴、y 轴的数据点和函数值。
- 返回类型:
tuple
示例
1>>> from pypop7.benchmarks import base_functions 2>>> from pypop7.benchmarks.utils import generate_xyz 3>>> x_, y_, z_ = generate_xyz(base_functions.sphere, [0.0, 1.0], [0.0, 1.0], num=2) 4>>> print(x_.shape, y_.shape, z_.shape)
- pypop7.benchmarks.utils.plot_contour(func, x, y, levels=None, num=200, is_save=False)[源代码]
绘制适应度地形的二维等高线图。
- 参数:
func (func) – 基准测试函数。
x (list) – x 轴范围。
y (list) – y 轴范围。
levels (int or list) – 等高线的数量或等高线列表。
num (int) – x 轴和 y 轴范围内的采样点数量(默认为 200)。
is_save (bool) – 是否将生成的图像保存在本地文件夹中(默认为 False)。
- 返回类型:
一个在线图像。
示例
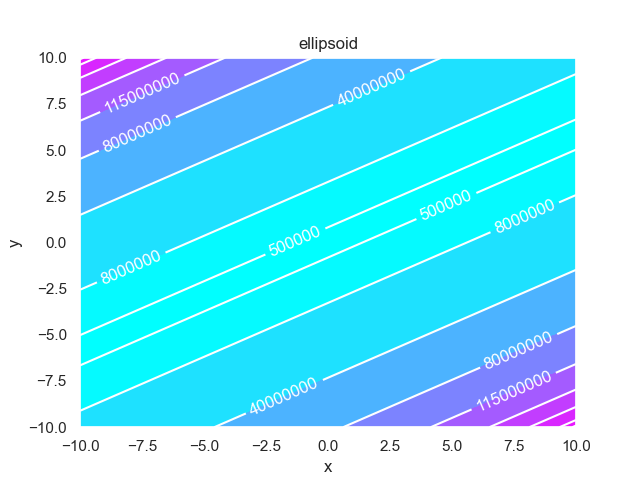
1>>> from pypop7.benchmarks.utils import plot_contour 2>>> from pypop7.benchmarks.rotated_functions import generate_rotation_matrix 3>>> from pypop7.benchmarks.rotated_functions import ellipsoid 4>>> # plot ill-condition and non-separability 5>>> generate_rotation_matrix(ellipsoid, 2, 72) 6>>> contour_levels = [0, 5e5, 8e6, 4e7, 8e7, 1.15e8, 1.42e8, 1.62e8, 1.78e8, 1.85e8, 2e8] 7>>> plot_contour(ellipsoid, [-10.0, 10.0], [-10.0, 10.0], contour_levels)
上述示例中生成的在线图像如下所示
绘制三维适应度地形图
- pypop7.benchmarks.utils.plot_surface(func, x, y, num=200, is_save=False)[源代码]
绘制适应度地形的三维曲面图。
- 参数:
func (func) – 基准测试函数。
x (list) – x 轴范围。
y (list) – y 轴范围。
num (int) – x 轴和 y 轴范围内的采样点数量(默认为 200)。
is_save (bool) – 是否将生成的图像保存在本地文件夹中(默认为 False)。
- 返回类型:
一个在线图像。
示例
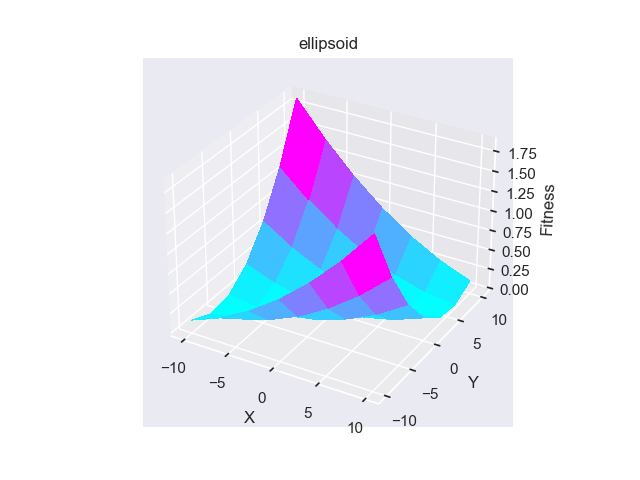
1>>> from pypop7.benchmarks.utils import plot_surface 2>>> from pypop7.benchmarks.rotated_functions import ellipsoid 3>>> from pypop7.benchmarks.rotated_functions import generate_rotation_matrix 4>>> # plot ill-condition and non-separability 5>>> generate_rotation_matrix(ellipsoid, 2, 72) 6>>> plot_surface(ellipsoid, [-10.0, 10.0], [-10.0, 10.0], 7)
上述示例中生成的在线图像如下所示
通过对象序列化保存优化结果
对于复杂对象的序列化,我们使用 Python 的标准库(pickle)。有关介绍,请参阅 Python wiki。
- pypop7.benchmarks.utils.save_optimization(results, algo, func, dim, exp, folder='pypop7_benchmarks_lso')[源代码]
通过对象序列化保存优化结果(以 pickle 格式)。
注意
默认情况下,要保存的本地文件名格式如下:Algo-{}_Func-{}_Dim-{}_Exp-{}.pickle,保存在本地文件夹 pypop7_benchmarks_lso 中。
- 参数:
results (dict) – 任何优化器返回的优化结果。
algo (str) – 要使用的算法名称。
func (str) – 要最小化的适应度函数名称。
dim (str or int) – 要最小化的适应度函数的维度。
exp (str or int) – 每次独立运行的实验索引。
folder (str) – 工作空间下的本地文件夹,可通过 pwd() 命令获取(默认为 pypop7_benchmarks_lso)。
- 返回类型:
一个存储在工作空间中的本地文件(可通过 pwd() 命令获取)。
示例
1>>> import numpy # engine for numerical computing 2>>> from pypop7.benchmarks.base_functions import rosenbrock # function to be minimized 3>>> from pypop7.optimizers.rs.prs import PRS 4>>> from pypop7.benchmarks.utils import save_optimization 5>>> ndim = 2 # number of dimensionality 6>>> problem = {'fitness_function': rosenbrock, # to define problem arguments 7... 'ndim_problem': ndim, 8... 'lower_boundary': -5.0 * numpy.ones((ndim,)), 9... 'upper_boundary': 5.0 * numpy.ones((ndim,))} 10>>> options = {'max_function_evaluations': 5000, # to set optimizer options 11... 'seed_rng': 2022} # global step-size may need to be tuned for optimality 12>>> prs = PRS(problem, options) # to initialize the black-box optimizer class 13>>> res = prs.optimize() # to run its optimization/evolution process 14>>> save_optimization(res, PRS.__name__, rosenbrock.__name__, ndim, 1)
请在通过 pwd() 命令获取的工作空间中检查以下本地文件
pypop7_benchmarks_lso/Algo-PRS_Func-rosenbrock_Dim-2_Exp-1.pickle
- pypop7.benchmarks.utils.read_optimization(folder, algo, func, dim, exp)[源代码]
在对象序列化后读取优化结果(以 pickle 格式)。
注意
默认情况下,要保存的本地文件名格式如下:Algo-{}_Func-{}_Dim-{}_Exp-{}.pickle,保存在本地文件夹中。
- 参数:
folder (str) – 工作空间下的本地文件夹,可通过 pwd() 命令获取。
algo (str) – 要使用的算法名称。
func (str) – 要最小化的适应度函数名称。
dim (str or int) – 要最小化的适应度函数的维度。
exp (str or int) – 每次独立运行的实验索引。
- 返回:
results – 任何优化器返回的优化结果。
- 返回类型:
dict
示例
1>>> import numpy # engine for numerical computing 2>>> from pypop7.benchmarks.base_functions import rosenbrock # function to be minimized 3>>> from pypop7.optimizers.rs.prs import PRS 4>>> from pypop7.benchmarks.utils import save_optimization, read_optimization 5>>> ndim = 2 # number of dimensionality 6>>> problem = {'fitness_function': rosenbrock, # to define problem arguments 7... 'ndim_problem': ndim, 8... 'lower_boundary': -5.0 * numpy.ones((ndim,)), 9... 'upper_boundary': 5.0 * numpy.ones((ndim,))} 10>>> options = {'max_function_evaluations': 5000, # to set optimizer options 11... 'seed_rng': 2022} # global step-size may need to be tuned for optimality 12>>> prs = PRS(problem, options) # to initialize the black-box optimizer class 13>>> res = prs.optimize() # to run its optimization/evolution process 14>>> save_optimization(res, PRS.__name__, rosenbrock.__name__, ndim, 1) 15>>> res = read_optimization('pypop7_benchmarks_lso', PRS.__name__, rosenbrock.__name__, ndim, 1) 16>>> print(res)
检查优化结果
- pypop7.benchmarks.utils.check_optimization(problem, options, results)[源代码]
根据问题参数和优化器选项检查优化结果。
- 参数:
problem (dict) – 问题参数。
options (dict) – 优化器选项。
results (dict) – 任何黑盒优化器生成的优化结果。
- 返回类型:
一份详细的检查报告。
示例
1>>> import numpy # engine for numerical computing 2>>> from pypop7.benchmarks.utils import check_optimization 3>>> pro = {'lower_boundary': [-5.0, -7.0, -3.0], 4... 'upper_boundary': [5.0, 7.0, 3.0]} 5>>> opt = {'max_function_evaluations': 7777777} 6>>> res = {'n_function_evaluations': 7777777, 7... 'best_so_far_x': numpy.zeros((3,))} 8>>> check_optimization(pro, opt, res)
通过 Matplotlib 绘制收敛曲线
这里我们使用 Matplotlib 为(仅)一个黑盒优化器绘制收敛曲线图。有关介绍,请参阅其官方网站。
- pypop7.benchmarks.utils.plot_convergence_curve(algo, func, dim, exp=1, results=None, folder='pypop7_benchmarks_lso')[源代码]
绘制一个优化器获得的最终优化结果的收敛曲线。
注意
默认情况下,要保存的本地文件名格式如下:Algo-{}_Func-{}_Dim-{}_Exp-{}.pickle,保存在本地文件夹 pypop7_benchmarks_lso 中。
- 参数:
algo (str) – 要使用的算法名称。
func (str) – 要最小化的适应度函数名称。
dim (str or int) – 要最小化的适应度函数的维度。
exp (str or int) – 要运行的实验索引。
results (dict) – 任何优化器返回的优化结果。
folder (str) – 工作空间下的本地文件夹(默认为 pypop7_benchmarks_lso)。
示例
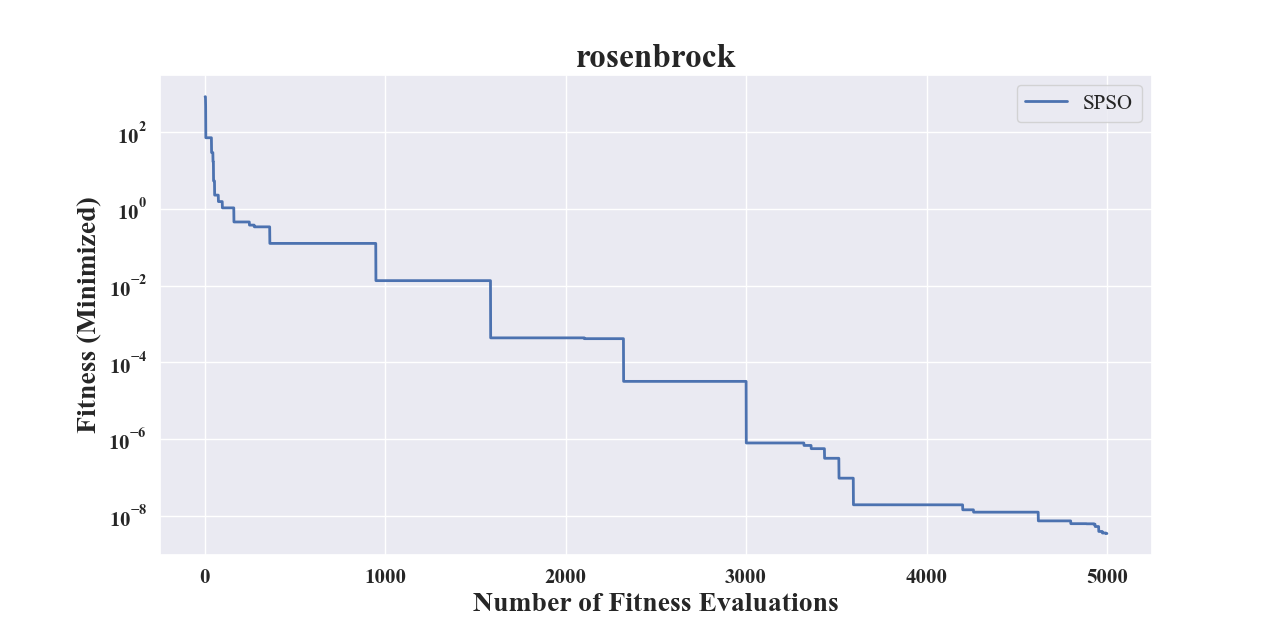
1>>> import numpy # engine for numerical computing 2>>> from pypop7.benchmarks.base_functions import rosenbrock # function to be minimized 3>>> from pypop7.optimizers.pso.spso import SPSO 4>>> from pypop7.benchmarks.utils import plot_convergence_curve 5>>> problem = {'fitness_function': rosenbrock, # to define problem arguments 6... 'ndim_problem': 2, 7... 'lower_boundary': -5.0*numpy.ones((2,)), 8... 'upper_boundary': 5.0*numpy.ones((2,))} 9>>> options = {'max_function_evaluations': 5000, # to set optimizer options 10... 'saving_fitness': 1, 11... 'seed_rng': 2022} 12>>> spso = SPSO(problem, options) # to initialize the black-box optimizer class 13>>> res = spso.optimize() # to run the optimization process 14>>> plot_convergence_curve('SPSO', rosenbrock.__name__, 2, results=res)
上述示例生成的在线图像如下所示
比较多个黑盒优化器
这里我们使用 Matplotlib 为多个黑盒优化器绘制收敛曲线图。
- pypop7.benchmarks.utils.plot_convergence_curves(algos, func, dim, exp=1, results=None, folder='pypop7_benchmarks_lso')[源代码]
绘制多个优化器获得的最终优化结果的收敛曲线。
注意
默认情况下,要保存的本地文件名格式如下:Algo-{}_Func-{}_Dim-{}_Exp-{}.pickle,保存在本地文件夹 pypop7_benchmarks_lso 中。
- 参数:
algos (list of class) – 要使用的优化器类列表。
func (str) – 要最小化的适应度函数名称。
dim (str or int) – 要最小化的适应度函数的维度。
exp (str or int) – 要运行的实验索引。
results (list of dict) – 任何优化器返回的优化结果。
folder (str) – 工作空间下的本地文件夹(默认为 pypop7_benchmarks_lso)。
示例
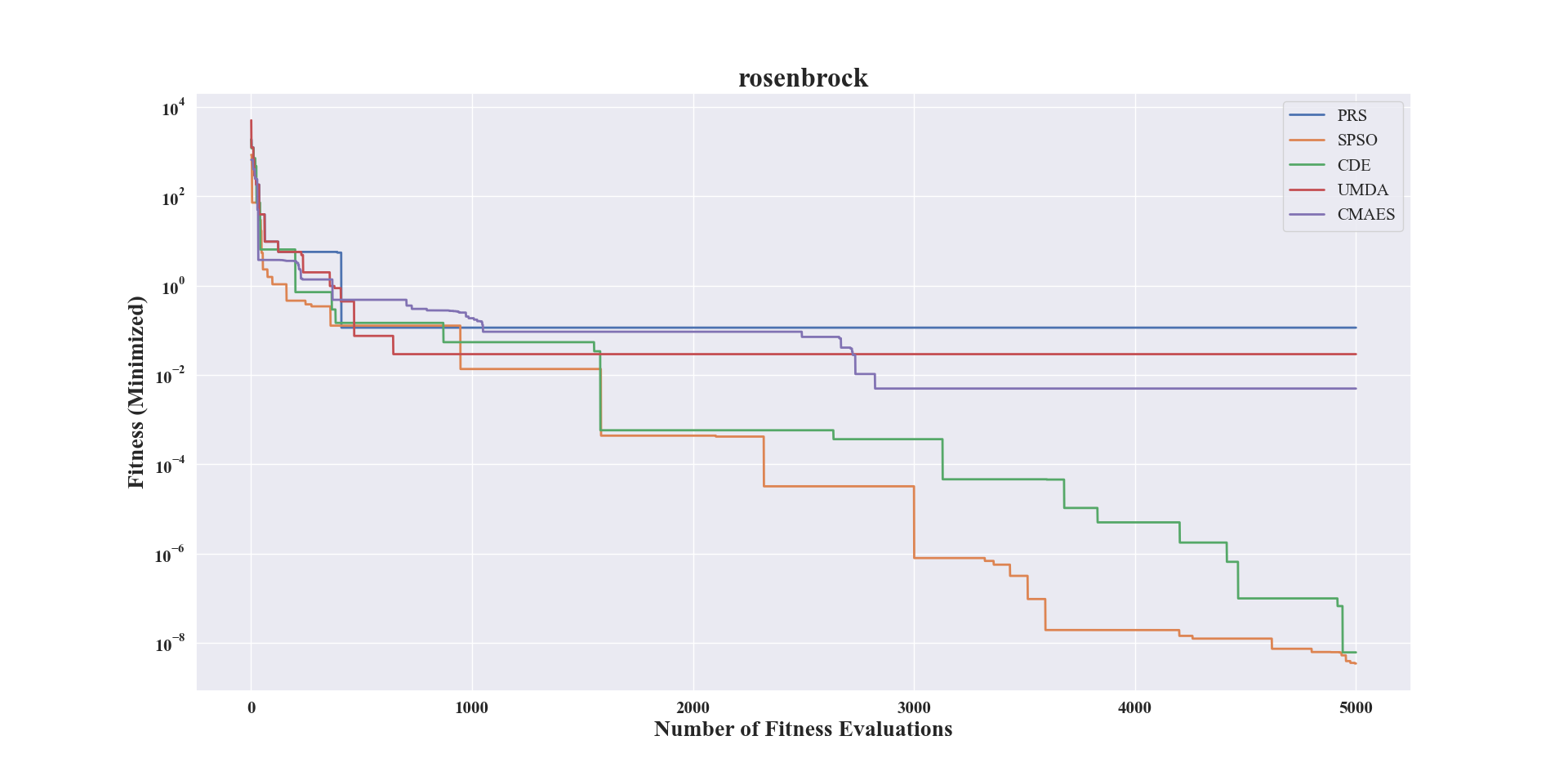
1>>> import numpy # engine for numerical computing 2>>> from pypop7.benchmarks.base_functions import rosenbrock # function to be minimized 3>>> from pypop7.optimizers.rs.prs import PRS 4>>> from pypop7.optimizers.pso.spso import SPSO 5>>> from pypop7.optimizers.de.cde import CDE 6>>> from pypop7.optimizers.eda.umda import UMDA 7>>> from pypop7.optimizers.es.cmaes import CMAES 8>>> from pypop7.benchmarks.utils import plot_convergence_curves 9>>> problem = {'fitness_function': rosenbrock, # to define problem arguments 10>>> 'ndim_problem': 2, 11>>> 'lower_boundary': -5.0*numpy.ones((2,)), 12>>> 'upper_boundary': 5.0*numpy.ones((2,))} 13>>> options = {'max_function_evaluations': 5000, # to set optimizer options 14>>> 'saving_fitness': 1, 15>>> 'sigma': 3.0, 16>>> 'seed_rng': 2022} 17>>> res = [] 18>>> for Optimizer in [PRS, SPSO, CDE, UMDA, CMAES]: 19>>> optimizer = Optimizer(problem, options) # to initialize the black-box optimizer class 20>>> res.append(optimizer.optimize()) # to run the optimization process 21>>> plot_convergence_curves([PRS, SPSO, CDE, UMDA, CMAES], rosenbrock.__name__, 2, results=res)
上述示例生成的在线图像如下所示
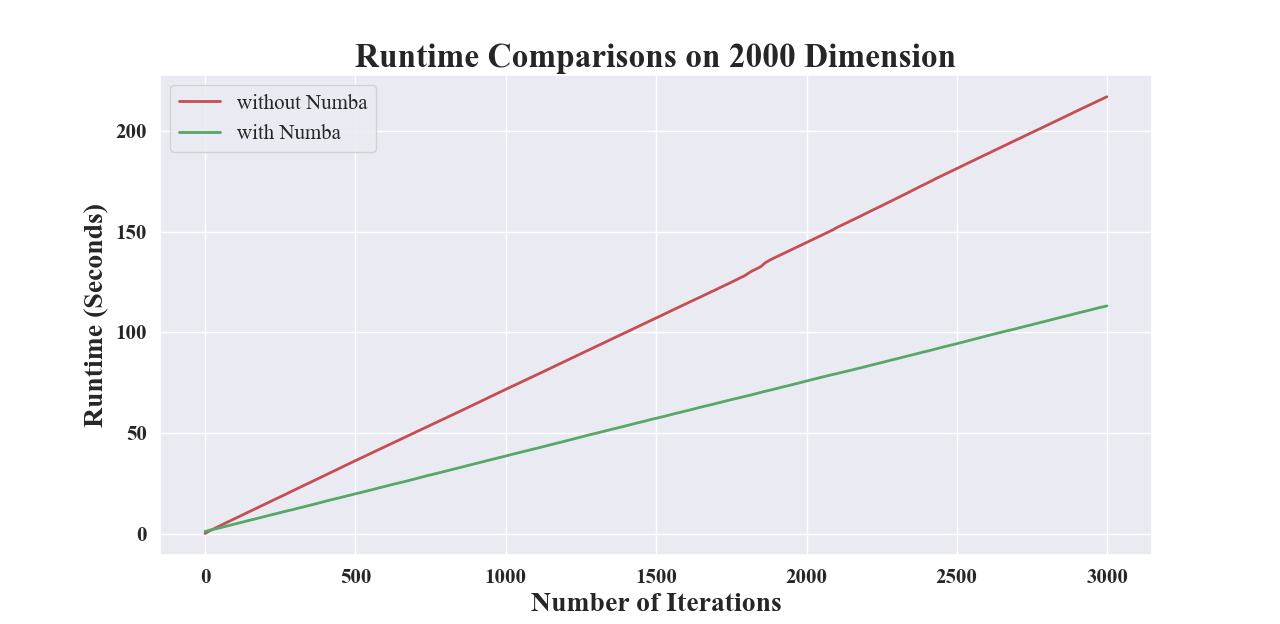
通过 Numba 加速计算
对于一些计算密集型操作,我们尽可能使用 Numba 来加速计算
- pypop7.benchmarks.utils.cholesky_update(rm, z, downdate)[源代码]
秩一矩阵的 Cholesky 更新。
- 参数:
rm ((N, N) ndarray) – 二维输入数据,将使用其三角部分读取 Cholesky 因子。
z ((N,) ndarray) – 一维更新/降级向量。
downdate (bool) – False 表示更新,而 True 表示降级(默认为 False)。
- 返回:
D – Cholesky 因子。
- 返回类型:
(N, N) ndarray
例如,对于秩一更新,使用与不使用 Numba 的运行时间比较如下所示