在线教程
在这里,我们提供了一些有趣的在线教程,以帮助更好地使用这个用于黑盒优化 (BBO) 的开源 Python 库 PyPop7,如下所示
来自 [Beyer, GECCO] 的透镜形状优化,
来自 pagmo(由欧洲航天局开发)的 Lennard-Jones 团簇优化,
来自 pykep(由欧洲航天局开发)的全局轨迹优化,
控制器设计/优化(又名直接策略搜索),
在精心设计的 COCO 平台上对 BBO 进行基准测试(COCO 荣获 SIGEVO 影响力奖),
对于这个开源库中的每个黑盒优化器,我们还在其相应的 API 文档中提供了一个玩具示例,并在其相应的 Python 源代码文件夹中提供了两个测试代码(如果可能)。
透镜形状优化
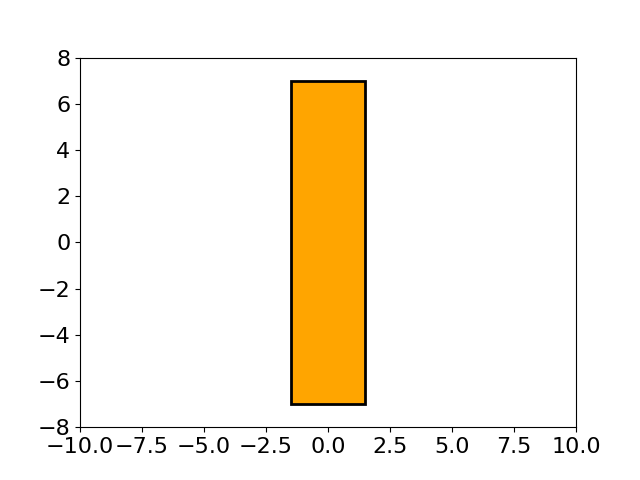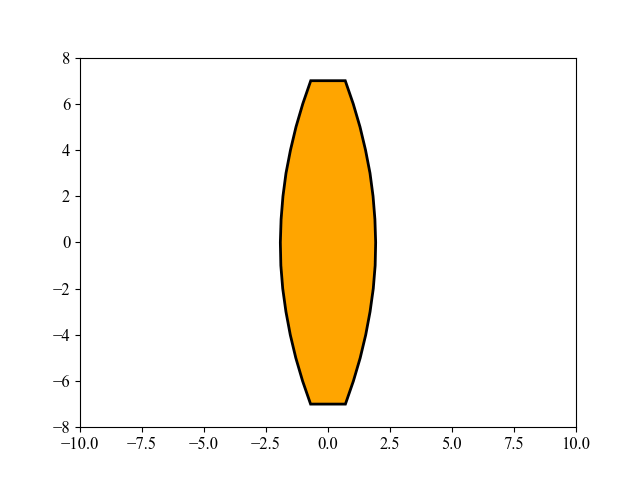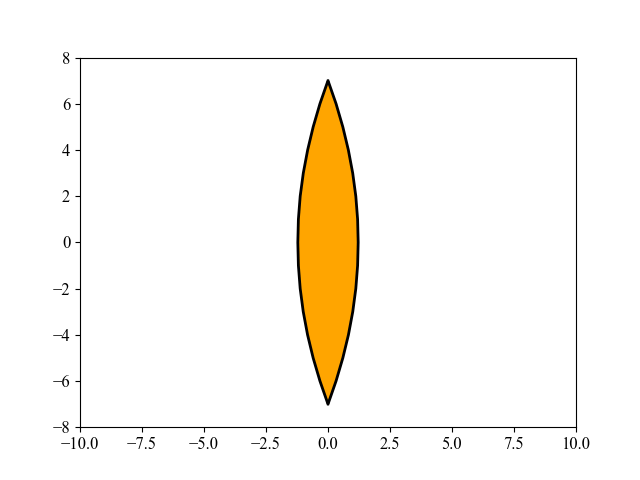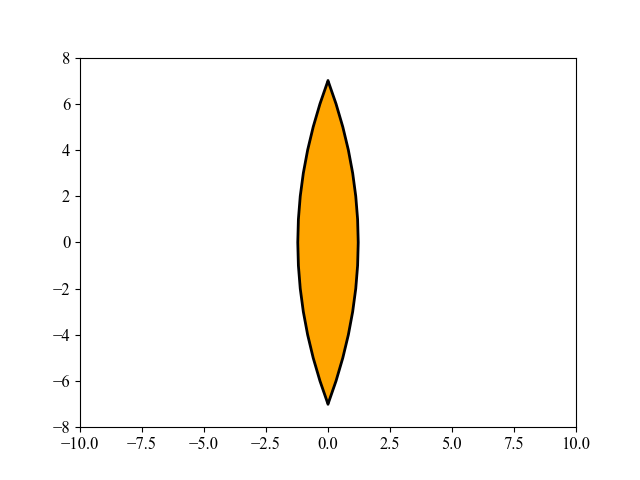
该图展示了由 MAES 优化的透镜形状演化过程,这是一个有趣的现象。MAES 是成熟的 CMA-ES 算法的一个简化现代版本(性能几乎没有明显损失)。其主要目标是找到玻璃体的最佳形状,使得平行入射的光线在平面上的一个给定点聚焦,同时使用尽可能少的玻璃材料。有关这里使用的 15 维目标函数的更多数学细节,请参阅 [Beyer, 2020, GECCO]。要重现上图,请运行以下 Python 代码
# Written/Checked by Guochen Zhou, Minghan Zhang, Yajing Tan, and *Qiqi Duan*
import numpy as np
import imageio.v2 as imageio # for animation
import matplotlib.pyplot as plt # for static plotting
from matplotlib.path import Path # for static plotting
import matplotlib.patches as patches # for static plotting
from pypop7.optimizers.es.es import ES # abstract class for all evolution Strategies
from pypop7.optimizers.es.maes import MAES # Matrix Adaptation Evolution Strategy
# <1> - Set Parameters for Lens Shape Optimization
weight = 0.9 # weight of focus function
r = 7 # radius of lens
h = 1 # trapezoidal slices of height
b = 20 # distance between lens and object
eps = 1.5 # refraction index
d_init = 3 # initialization
# <2> - Define Objective Function (aka Fitness Function) to be *Minimized*
def func_lens(x): # refer to [Beyer, 2020, ACM-GECCO] for all mathematical details
n = len(x)
focus = r - ((h*np.arange(1, n) - 0.5) + b/h*(eps - 1)*np.transpose(np.abs(x[1:]) - np.abs(x[:(n-1)])))
mass = h*(np.sum(np.abs(x[1:(n-1)])) + 0.5*(np.abs(x[0]) + np.abs(x[n-1])))
return weight*np.sum(focus**2) + (1.0 - weight)*mass
def get_path(x): # only for plotting
left, right, height = [], [], r
for i in range(len(x)):
x[i] = -x[i] if x[i] < 0 else x[i]
left.append((-0.5*x[i], height))
right.append((0.5*x[i], height))
height -= 1
points = left
for i in range(len(right)):
points.append(right[-i - 1])
points.append(left[0])
codes = [Path.MOVETO]
for i in range(len(points) - 2):
codes.append(Path.LINETO)
codes.append(Path.CLOSEPOLY)
return Path(points, codes)
def plot(xs):
file_names, frames = [], []
for i in range(len(xs)):
sub_figure = '_' + str(i) + '.png'
fig = plt.figure()
ax = fig.add_subplot(111)
plt.rcParams['font.family'] = 'Times New Roman'
plt.rcParams['font.size'] = '12'
ax.set_xlim(-10, 10)
ax.set_ylim(-8, 8)
path = get_path(xs[i])
patch = patches.PathPatch(path, facecolor='orange', lw=2)
ax.add_patch(patch)
plt.savefig(sub_figure)
file_names.append(sub_figure)
for image in file_names:
frames.append(imageio.imread(image))
imageio.mimsave('lens_shape_optimization.gif', frames, 'GIF', duration=0.3)
# <3> - Extend Optimizer Class MAES to Generate Data for Plotting
class MAESPLOT(MAES): # to overwrite original MAES algorithm for plotting
def optimize(self, fitness_function=None, args=None): # for all generations (iterations)
fitness = ES.optimize(self, fitness_function)
z, d, mean, s, tm, y = self.initialize()
xs = [mean.copy()] # for plotting
while not self._check_terminations():
z, d, y = self.iterate(z, d, mean, tm, y, args)
if self.saving_fitness and (not self._n_generations % self.saving_fitness):
xs.append(self.best_so_far_x) # for plotting
mean, s, tm = self._update_distribution(z, d, mean, s, tm, y)
self._print_verbose_info(fitness, y)
self._n_generations += 1
if self.is_restart:
z, d, mean, s, tm, y = self.restart_reinitialize(z, d, mean, s, tm, y)
res = self._collect(fitness, y, mean)
res['xs'] = xs # for plotting
return res
if __name__ == '__main__':
ndim_problem = 15 # dimension of objective function
problem = {'fitness_function': func_lens, # objective (fitness) function
'ndim_problem': ndim_problem, # number of dimensionality of objective function
'lower_boundary': -5.0*np.ones((ndim_problem,)), # lower boundary of search range
'upper_boundary': 5.0*np.ones((ndim_problem,))} # upper boundary of search range
options = {'max_function_evaluations': 7e3, # maximum of function evaluations
'seed_rng': 2022, # seed of random number generation (for repeatability)
'x': d_init*np.ones((ndim_problem,)), # initial mean of Gaussian search distribution
'sigma': 0.3, # global step-size of Gaussian search distribution (not necessarily an optimal value)
'saving_fitness': 50, # to record best-so-far fitness every 50 function evaluations
'is_restart': False} # whether or not to run the (default) restart process
results = MAESPLOT(problem, options).optimize()
plot(results['xs'])
正如达尔文所写,“如果能证明任何复杂的器官存在,而它不可能由无数、连续、微小的修改形成,我的理论就绝对会被推翻。” 幸运的是,从纯粹的优化(而非生物学)角度来看,眼镜片的演化确实可以通过许多小步骤来进行。
关于 ES / CMA-ES / NES 在许多挑战性优化问题上的更多有趣应用,请参考例如:[Lee et al., 2023, Science Robotics]; [Sun et al., 2023, ACL]; [Koginov et al., 2023, IEEE-TMRB]; [Lange et al., 2023, ICLR]; [Yu et al., 2023, IJCAI]; [Kim et al., 2023, Science Robotics]; [Slade et al., 2022, Nature]; [De Croon et al., 2022, Nature]; [Sun et al., 2022, ICML]; [Wang&Ponce, 2022, GECCO]; [Bharti et al., 2022, Rev. Mod. Phys]; [Nomura et al., 2021, AAAI], [Anand et al., 2021, Mach. Learn.: Sci. Technol.], [Maheswaranathan et al., 2019, ICML], [Dong et al., 2019, CVPR]; [Ha&Schmidhuber, 2018, NeurIPS]; [OpenAI, 2017], [Zhang et al., 2017, Science], [Agrawal et al., 2014, TVCG], [Koumoutsakos et al., 2001, AIAA], [Lipson&Pollack, 2000, Nature],仅举几例。关于顶级期刊/会议论文的系统性收集,请参阅 https://github.com/Evolutionary-Intelligence/DistributedEvolutionaryComputation。
Lennard-Jones 团簇优化
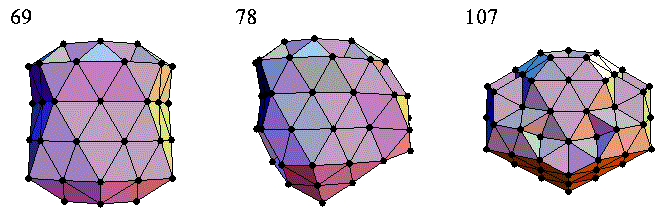
请注意,上图(即三个原子团簇)直接取自牛津大学的 Jonathan Doye 教授。在化学中,Lennard-Jones 团簇优化是一个流行的单目标实参数(黑盒)优化问题,其目标是假设每对原子之间存在 Lennard-Jones 势能,来最小化原子团簇的能量。在这里,我们使用两种不同的差分进化 (DE) 版本来解决这个高维优化问题。
import pygmo as pg # need to be installed: https://esa.github.io/pygmo2/install.html import seaborn as sns import matplotlib.pyplot as plt from pypop7.optimizers.de.cde import CDE # https://pypop.cn/en/latest/de/cde.html from pypop7.optimizers.de.jade import JADE # https://pypop.cn/en/latest/de/jade.html # see https://esa.github.io/pagmo2/docs/cpp/problems/lennard_jones.html for the fitness function prob = pg.problem(pg.lennard_jones(150)) print(prob) # 444-dimensional def energy_func(x): # wrapper to obtain fitness of type `float` return float(prob.fitness(x)) if __name__ == '__main__': results = [] # to save all optimization results from different optimizers for DE in [CDE, JADE]: problem = {'fitness_function': energy_func, 'ndim_problem': 444, 'upper_boundary': prob.get_bounds()[1], 'lower_boundary': prob.get_bounds()[0]} if DE == JADE: # for JADE (but not for CDE) is_bound = True else: is_bound = False options = {'max_function_evaluations': 400000, 'seed_rng': 2022, # for repeatability 'saving_fitness': 1, # to save all fitness generated during optimization 'is_bound': is_bound} solver = DE(problem, options) results.append(solver.optimize()) print(results[-1]) sns.set_theme(style='darkgrid') plt.figure() for label, res in zip(['CDE', 'JADE'], results): plt.plot(res['fitness'][250000:, 0], res['fitness'][250000:, 1], label=label) plt.legend() plt.show()
为 CDE(无边界约束)和 JADE(有边界约束)生成的两条收敛曲线如下图所示(从第 250000 代开始可以避免早期阶段产生的过高适应度值扰乱收敛曲线)
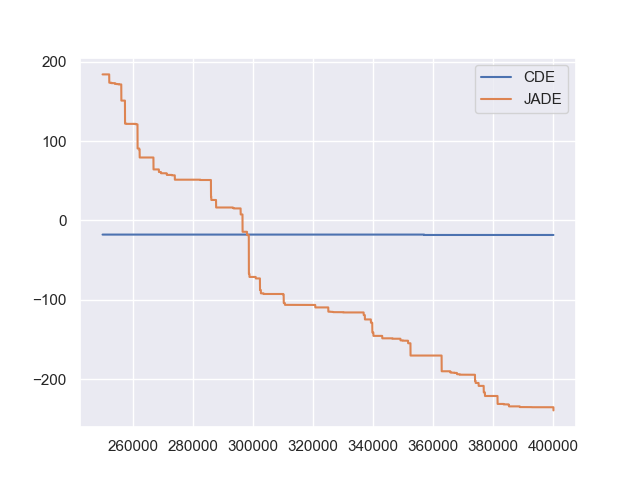
从上图可以看出,两种不同的 DE 版本表现出不同的搜索性能:CDE 在优化过程中不限制样本在给定的搜索边界内,并非常快地生成一个超出边界的解(这在实践中可能是不可行的),而 JADE 在优化过程中将所有样本限制在给定的搜索边界内,并相对较慢地生成一个边界内的解。由于同一算法家族的不同实现有时甚至可能导致完全不同的搜索行为,因此其开源实现对于可重复性至关重要。
关于 DE 在挑战性问题上的更多有趣应用,请参考例如:[Higgins et al., 2023, Science]; [McNulty et al., 2023, PRL]; [An et al., 2020, PNAS]; [Gagnon et al., 2017, PRL]; [Laganowsky et al., 2014, Nature]; [Lovett et al., 2013, PRL],仅举几例。关于顶级期刊/会议上演化算法论文的系统性收集,请参阅 https://github.com/Evolutionary-Intelligence/DistributedEvolutionaryComputation。
PyKep 的全局轨迹优化
在欧洲航天局开发的 pykep 中,给出了六个困难的全局轨迹优化 (GTO) 问题。在这里,我们使用标准粒子群优化器(SPSO)作为黑盒优化器的基准。
"""Demo that uses PSO to optimize 6 GTO problems provided by `pykep`: https://esa.github.io/pykep/ https://esa.github.io/pykep/examples/ex13.html """ import pygmo as pg # it's better to use conda to install (and it's better to use pygmo==2.18) import pykep as pk # it's better to use conda to install import matplotlib.pyplot as plt from pypop7.optimizers.pso.spso import SPSO as Solver fig, axes = plt.subplots(nrows=3, ncols=2, sharex='col', sharey='row', figsize=(15, 15)) problems = [pk.trajopt.gym.cassini2, pk.trajopt.gym.eve_mga1dsm, pk.trajopt.gym.messenger, pk.trajopt.gym.rosetta, pk.trajopt.gym.em5imp, pk.trajopt.gym.em7imp] ticks = [0, 5e3, 1e4, 1.5e4, 2e4] for prob_number in range(0, 6): udp = problems[prob_number] def fitness_func(x): # wrapper of fitness function return udp.fitness(x)[0] prob = pg.problem(udp) print(prob) pro = {'fitness_function': fitness_func, 'ndim_problem': prob.get_nx(), 'lower_boundary': prob.get_lb(), 'upper_boundary': prob.get_ub()} opt = {'seed_rng': 0, 'max_function_evaluations': 2e4, 'saving_fitness': 1, 'is_bound': True} solver = Solver(pro, opt) res = solver.optimize() if prob_number == 0: axes[0, 0].semilogy(res['fitness'][:, 0], res['fitness'][:, 1], '--', color='fuchsia', label='SPSO') axes[0, 0].set_title('cassini2') elif prob_number == 1: axes[0, 1].semilogy(res['fitness'][:, 0], res['fitness'][:, 1], '--', color='royalblue', label='SPSO') axes[0, 1].set_title('eve_mga1dsm') elif prob_number == 2: axes[1, 0].semilogy(res['fitness'][:, 0], res['fitness'][:, 1], '--', color='deepskyblue', label='SPSO') axes[1, 0].set_title('messenger') elif prob_number == 3: axes[1, 1].semilogy(res['fitness'][:, 0], res['fitness'][:, 1], '--', color='lime', label='SPSO') axes[1, 1].set_title('rosetta') elif prob_number == 4: axes[2, 0].semilogy(res['fitness'][:, 0], res['fitness'][:, 1], '--', color='darkorange', label='SPSO') axes[2, 0].set_title('em5imp') elif prob_number == 5: axes[2, 1].semilogy(res['fitness'][:, 0], res['fitness'][:, 1], '--', color='brown', label='SPSO') axes[2, 1].set_title('em7imp') for ax in axes.flat: ax.set(xlabel='Function Evaluations', ylabel='Fitness [m/s]') ax.set_xticks(ticks) ax.grid() plt.savefig('pykep_optimization.jpg') # to save locally
通过 SPSO 在六个不同实例上获得的收敛曲线如下所示。
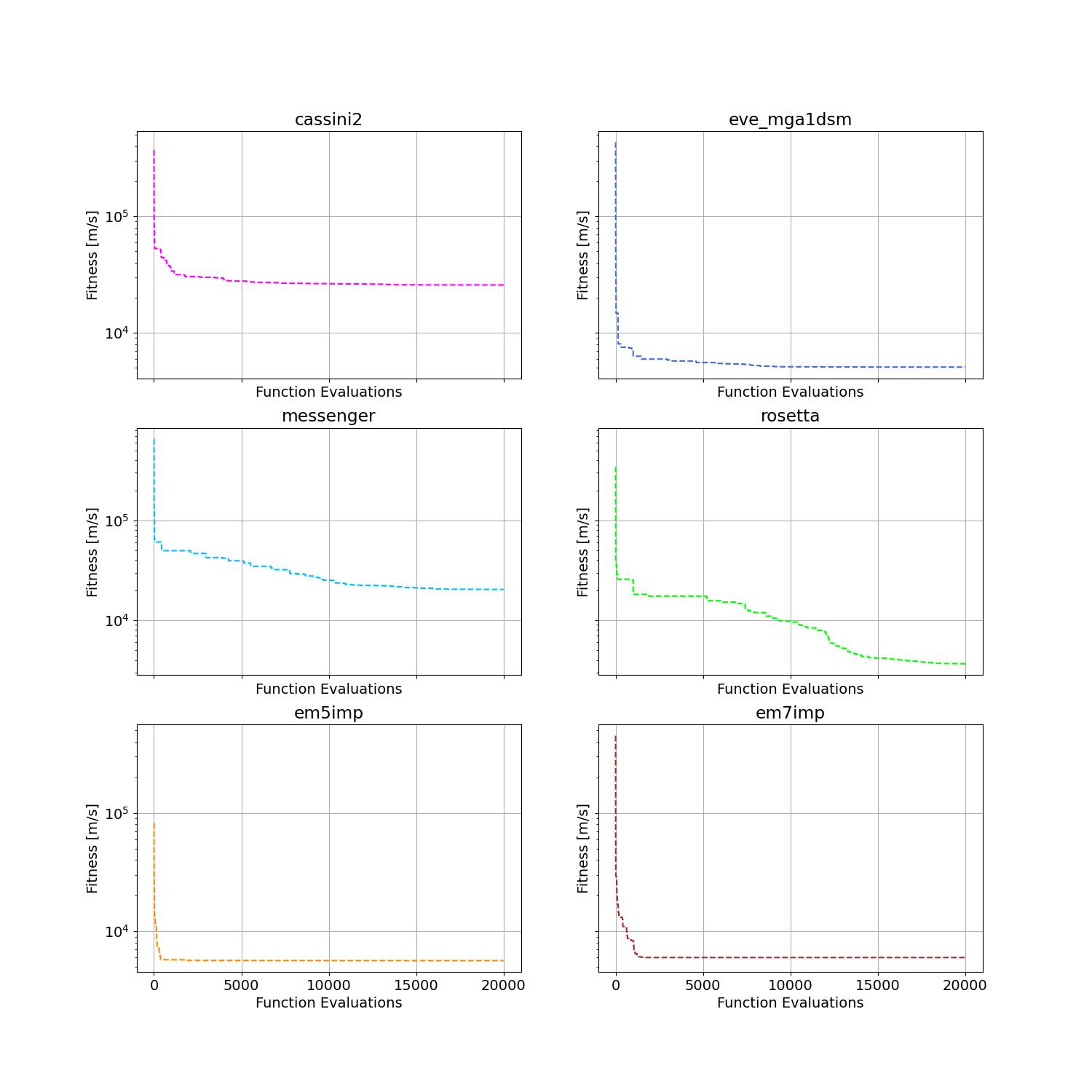
关于 PSO 在一些挑战性问题上的更多应用,请参考例如:[Reddy et al., 2023, TC]; [Guan et al., 2022, PRL]; [Weiel, et al., 2021, Nature Mach. Intell.]; [Tang et al., 2019, TPAMI]; [ Villeneuve et al., 2017, Science]; [Zhang et al., 2015, IJCV]; [Sharp et al., 2015, CHI]; [Tompson et al., 2014, TOG]; [Baca et al., 2013, Cell]; [Kim et al., 2012, Nature]; 仅举几例。关于顶级期刊/会议论文的系统性收集,请参阅 https://github.com/Evolutionary-Intelligence/DistributedEvolutionaryComputation。
大规模黑盒优化 (LBO) 基准测试
BBO 算法的基准测试在理解其搜索动态、比较其竞争性能、分析其优缺点以及在应用于挑战性现实世界问题之前选择其最新版本(SOTA)方面扮演着至关重要的角色。
注意
“一个有偏见的基准,排除了大部分现实世界的需求,会导致有偏见的结论,无论我们进行多少实验。” —[Meunier et al., 2022, TEVC]
这里我们展示了如何在一组相对较大的 LBO 测试函数集上对多个黑盒优化器进行基准测试,以便主要比较它们的局部搜索能力。
首先,作为标准的基准测试实践,生成实验中所需的平移向量和旋转矩阵,用于避免可能对中心和可分性的偏见。
import time import numpy as np from pypop7.benchmarks.shifted_functions import generate_shift_vector from pypop7.benchmarks.rotated_functions import generate_rotation_matrix def generate_sv_and_rm(functions=None, ndims=None, seed=None): if functions is None: functions = ['sphere', 'cigar', 'discus', 'cigar_discus', 'ellipsoid', 'different_powers', 'schwefel221', 'step', 'rosenbrock', 'schwefel12'] if ndims is None: ndims = [2, 10, 100, 200, 1000, 2000] if seed is None: seed = 20221001 rng = np.random.default_rng(seed) seeds = rng.integers(np.iinfo(np.int64).max, size=(len(functions), len(ndims))) for i, f in enumerate(functions): for j, d in enumerate(ndims): generate_shift_vector(f, d, -9.5, 9.5, seeds[i, j]) start_run = time.time() for i, f in enumerate(functions): for j, d in enumerate(ndims): start_time = time.time() generate_rotation_matrix(f, d, seeds[i, j]) print('* {:d}-d {:s}: runtime {:7.5e}'.format( d, f, time.time() - start_time)) print('*** Total runtime: {:7.5e}.'.format(time.time() - start_run)) if __name__ == '__main__': generate_sv_and_rm()
然后,在这些(经过旋转和平移的)测试函数上调用 PyPop7 中的多个黑盒优化器。
import os import time import pickle import argparse import numpy as np import pypop7.benchmarks.continuous_functions as cf class Experiment(object): def __init__(self, index, function, seed, ndim_problem): self.index, self.seed = index, seed self.function, self.ndim_problem = function, ndim_problem # save all data generated during optimization self._folder = 'pypop7_benchmarks_lso' if not os.path.exists(self._folder): os.makedirs(self._folder) # set file format self._file = os.path.join(self._folder, 'Algo-{}_Func-{}_Dim-{}_Exp-{}.pickle') def run(self, optimizer): problem = {'fitness_function': self.function, 'ndim_problem': self.ndim_problem, 'upper_boundary': 10.0 * np.ones((self.ndim_problem,)), 'lower_boundary': -10.0 * np.ones((self.ndim_problem,))} options = {'max_function_evaluations': 100000 * self.ndim_problem, 'max_runtime': 3600 * 3, # seconds (=3 hours) 'fitness_threshold': 1e-10, 'seed_rng': self.seed, 'sigma': 20.0 / 3.0, 'saving_fitness': 2000, 'verbose': 0} options['temperature'] = 100.0 # for simulated annealing (SA) solver = optimizer(problem, options) results = solver.optimize() file = self._file.format(solver.__class__.__name__, solver.fitness_function.__name__, solver.ndim_problem, self.index) with open(file, 'wb') as handle: # data format (pickle) pickle.dump(results, handle, protocol=pickle.HIGHEST_PROTOCOL) class Experiments(object): def __init__(self, start, end, ndim_problem): self.start, self.end = start, end self.ndim_problem = ndim_problem self.functions = [cf.sphere, cf.cigar, cf.discus, cf.cigar_discus, cf.ellipsoid, cf.different_powers, cf.schwefel221, cf.step, cf.rosenbrock, cf.schwefel12] # set RNG seeds for repeatability self.seeds = np.random.default_rng(2022).integers( np.iinfo(np.int64).max, size=(len(self.functions), 50)) def run(self, optimizer): for index in range(self.start, self.end + 1): print('* experiment: {:d} ***:'.format(index)) for i, f in enumerate(self.functions): start_time = time.time() print(' * function: {:s}:'.format(f.__name__)) experiment = Experiment(index, f, self.seeds[i, index], self.ndim_problem) experiment.run(optimizer) print(' runtime: {:7.5e}.'.format(time.time() - start_time)) if __name__ == '__main__': start_runtime = time.time() parser = argparse.ArgumentParser() # set starting index of experiments (from 0 to 49) parser.add_argument('--start', '-s', type=int) # set ending index of experiments (from 0 to 49) parser.add_argument('--end', '-e', type=int) # use any optimizer from PyPop7 parser.add_argument('--optimizer', '-o', type=str) # set dimension of all fitness functions parser.add_argument('--ndim_problem', '-d', type=int, default=2000) args = parser.parse_args() params = vars(args) # ensure seeds between 0 (include) and 49 (include) assert isinstance(params['start'], int) and 0 <= params['start'] < 50 assert isinstance(params['end'], int) and 0 <= params['end'] < 50 assert isinstance(params['optimizer'], str) assert isinstance(params['ndim_problem'], int) and params['ndim_problem'] > 0 if params['optimizer'] == 'PRS': # 1952 # PRS: Ashby's "Design for a Brain: The Origin of Adaptive Behavior" # (1952 - 1st Edition / 1960 - 2nd Edition) # https://link.springer.com/book/10.1007/978-94-015-1320-3 from pypop7.optimizers.rs.prs import PRS as Optimizer elif params['optimizer'] == 'SRS': # 2001 from pypop7.optimizers.rs.srs import SRS as Optimizer elif params['optimizer'] == 'ARHC': # 2008 from pypop7.optimizers.rs.arhc import ARHC as Optimizer elif params['optimizer'] == 'GS': # 2017 from pypop7.optimizers.rs.gs import GS as Optimizer elif params['optimizer'] == 'BES': from pypop7.optimizers.rs.bes import BES as Optimizer elif params['optimizer'] == 'HJ': from pypop7.optimizers.ds.hj import HJ as Optimizer elif params['optimizer'] == 'NM': from pypop7.optimizers.ds.nm import NM as Optimizer elif params['optimizer'] == 'POWELL': from pypop7.optimizers.ds.powell import POWELL as Optimizer elif params['optimizer'] == 'FEP': from pypop7.optimizers.ep.fep import FEP as Optimizer elif params['optimizer'] == 'GENITOR': from pypop7.optimizers.ga.genitor import GENITOR as Optimizer elif params['optimizer'] == 'G3PCX': from pypop7.optimizers.ga.g3pcx import G3PCX as Optimizer elif params['optimizer'] == 'GL25': from pypop7.optimizers.ga.gl25 import GL25 as Optimizer elif params['optimizer'] == 'COCMA': from pypop7.optimizers.cc.cocma import COCMA as Optimizer elif params['optimizer'] == 'HCC': from pypop7.optimizers.cc.hcc import HCC as Optimizer elif params['optimizer'] == 'SPSO': from pypop7.optimizers.pso.spso import SPSO as Optimizer elif params['optimizer'] == 'SPSOL': from pypop7.optimizers.pso.spsol import SPSOL as Optimizer elif params['optimizer'] == 'CLPSO': from pypop7.optimizers.pso.clpso import CLPSO as Optimizer elif params['optimizer'] == 'CCPSO2': from pypop7.optimizers.pso.ccpso2 import CCPSO2 as Optimizer elif params['optimizer'] == 'CDE': from pypop7.optimizers.de.cde import CDE as Optimizer elif params['optimizer'] == 'JADE': from pypop7.optimizers.de.jade import JADE as Optimizer elif params['optimizer'] == 'SHADE': from pypop7.optimizers.de.shade import SHADE as Optimizer elif params['optimizer'] == 'SCEM': from pypop7.optimizers.cem.scem import SCEM as Optimizer elif params['optimizer'] == 'MRAS': from pypop7.optimizers.cem.mras import MRAS as Optimizer elif params['optimizer'] == 'DSCEM': from pypop7.optimizers.cem.dscem import DSCEM as Optimizer elif params['optimizer'] == 'UMDA': from pypop7.optimizers.eda.umda import UMDA as Optimizer elif params['optimizer'] == 'EMNA': from pypop7.optimizers.eda.emna import EMNA as Optimizer elif params['optimizer'] == 'RPEDA': from pypop7.optimizers.eda.rpeda import RPEDA as Optimizer elif params['optimizer'] == 'XNES': from pypop7.optimizers.nes.xnes import XNES as Optimizer elif params['optimizer'] == 'SNES': from pypop7.optimizers.nes.snes import SNES as Optimizer elif params['optimizer'] == 'R1NES': from pypop7.optimizers.nes.r1nes import R1NES as Optimizer elif params['optimizer'] == 'CMAES': from pypop7.optimizers.es.cmaes import CMAES as Optimizer elif params['optimizer'] == 'FMAES': from pypop7.optimizers.es.fmaes import FMAES as Optimizer elif params['optimizer'] == 'RMES': from pypop7.optimizers.es.rmes import RMES as Optimizer elif params['optimizer'] == 'VDCMA': from pypop7.optimizers.es.vdcma import VDCMA as Optimizer elif params['optimizer'] == 'LMMAES': from pypop7.optimizers.es.lmmaes import LMMAES as Optimizer elif params['optimizer'] == 'MMES': from pypop7.optimizers.es.mmes import MMES as Optimizer elif params['optimizer'] == 'LMCMA': from pypop7.optimizers.es.lmcma import LMCMA as Optimizer elif params['optimizer'] == 'LAMCTS': from pypop7.optimizers.bo.lamcts import LAMCTS as Optimizer else: raise ValueError(f"Cannot find optimizer class {params['optimizer']} in PyPop7!") experiments = Experiments(params['start'], params['end'], params['ndim_problem']) experiments.run(Optimizer) print('Total runtime: {:7.5e}.'.format(time.time() - start_runtime))
请在高性能计算服务器上后台运行以上 Python 脚本(此处命名为 run_experiments.py),因为 LBO 通常需要很长的运行时间。
$ # on Linux $ nohup python run_experiments.py -s=1 -e=2 -o=LMCMA >LMCMA_1_2.out 2>&1 &
为了进一步比较不同黑盒优化器在 LBO 上的全局搜索能力,请使用基准测试套件:benchmark_global_search()。
控制器设计/优化
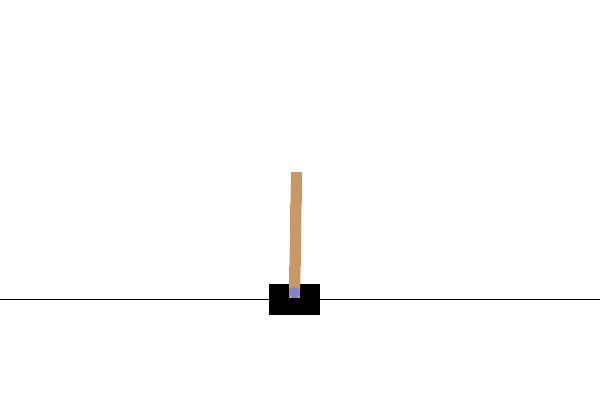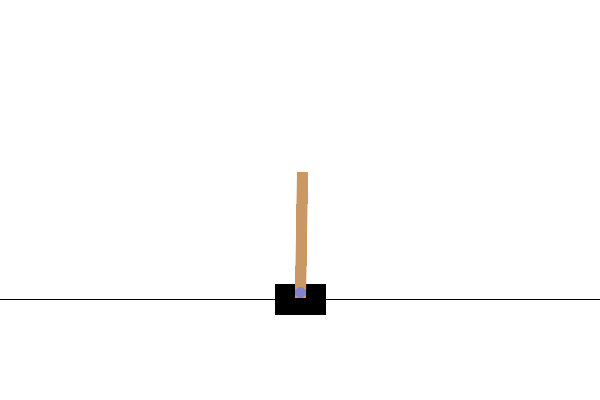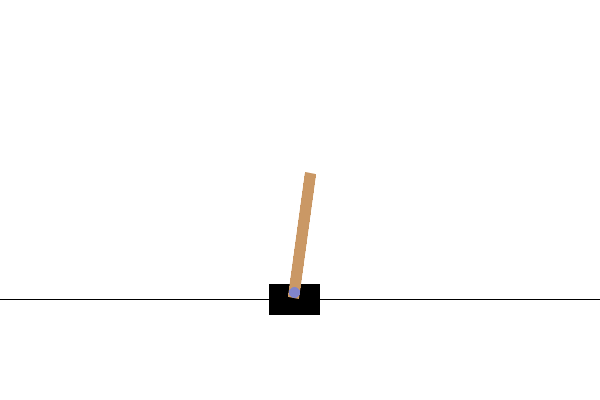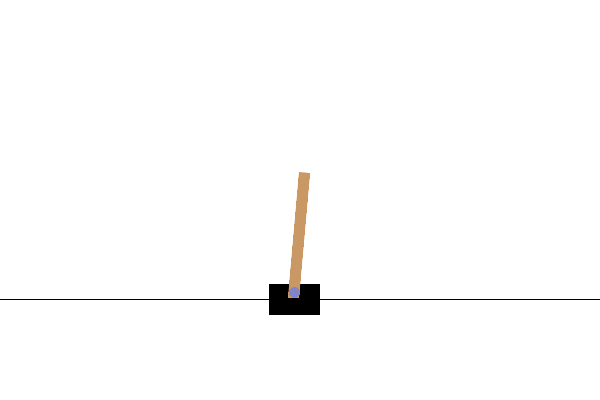
使用基于群体的(例如,演化)优化方法来设计机器人控制器已有较长的历史。最近,分布式计算的日益普及使其成为强化学习(RL)的一个有竞争力的替代方案,正如 OpenAI 2017 年的研究报告所实证的那样。在这里,我们提供一个非常简化的演示,展示 ES 如何在一个名为 CartPole 的经典控制问题上表现良好。
"""This is a simple demo to optimize a linear controller on the popular `gymnasium` platform for RL: https://github.com/Farama-Foundation/Gymnasium $ pip install gymnasium $ pip install gymnasium[classic-control] For benchmarking, please use more challenging MuJoCo tasks: https://mujoco.cn/ """ import numpy as np # to be installed from https://github.com/Farama-Foundation/Gymnasium import gymnasium as gym from pypop7.optimizers.es.maes import MAES as Solver class Controller: # linear controller for simplicity def __init__(self): self.env = gym.make('CartPole-v1', render_mode='human') self.observation, _ = self.env.reset() # for action probability space self.action_dim = self.env.action_space.n def __call__(self, x): rewards = 0 self.observation, _ = self.env.reset() for i in range(1000): action = np.matmul(x.reshape(self.action_dim, -1), self.observation[:, np.newaxis]) actions = np.sum(action) prob_left, prob_right = action[0]/actions, action[1]/actions # seen as a probability action = 1 if prob_left < prob_right else 0 self.observation, reward, terminated, truncated, _ = self.env.step(action) rewards += reward if terminated or truncated: return -rewards # for minimization (rather than maximization) return -rewards # to negate rewards if __name__ == '__main__': c = Controller() pro = {'fitness_function': c, 'ndim_problem': len(c.observation)*c.action_dim, 'lower_boundary': -10*np.ones((len(c.observation)*c.action_dim,)), 'upper_boundary': 10*np.ones((len(c.observation)*c.action_dim,))} opt = {'max_function_evaluations': 1e4, 'seed_rng': 0, 'sigma': 3.0, 'verbose': 1} solver = Solver(pro, opt) print(solver.optimize()) c.env.close()
在精心设计的 COCO 平台上对 BBO 进行基准测试
在演化计算领域,COCO 是一个设计精良且积极维护的软件平台,用于在黑盒设置下比较连续优化器。
"""Demo for `COCO` benchmarking using only `PyPop7` here: https://github.com/numbbo/coco To install `COCO` successfully, please read the above open link carefully. """ import os import webbrowser # for post-processing in the browser import numpy as np import cocoex # experimentation module of `COCO` import cocopp # post-processing module of `COCO` from pypop7.optimizers.es.maes import MAES if __name__ == '__main__': suite, output = 'bbob', 'COCO-PyPop7-MAES' budget_multiplier = 1e3 # or 1e4, 1e5, ... observer = cocoex.Observer(suite, 'result_folder: ' + output) minimal_print = cocoex.utilities.MiniPrint() for function in cocoex.Suite(suite, '', ''): function.observe_with(observer) # to generate data for `cocopp` post-processing sigma = np.min(function.upper_bounds - function.lower_bounds) / 3.0 problem = {'fitness_function': function, 'ndim_problem': function.dimension, 'lower_boundary': function.lower_bounds, 'upper_boundary': function.upper_bounds} options = {'max_function_evaluations': function.dimension * budget_multiplier, 'seed_rng': 2022, 'x': function.initial_solution, 'sigma': sigma} solver = MAES(problem, options) print(solver.optimize()) cocopp.main(observer.result_folder) webbrowser.open('file://' + os.getcwd() + '/ppdata/index.html')
上述代码的最终输出如下所示

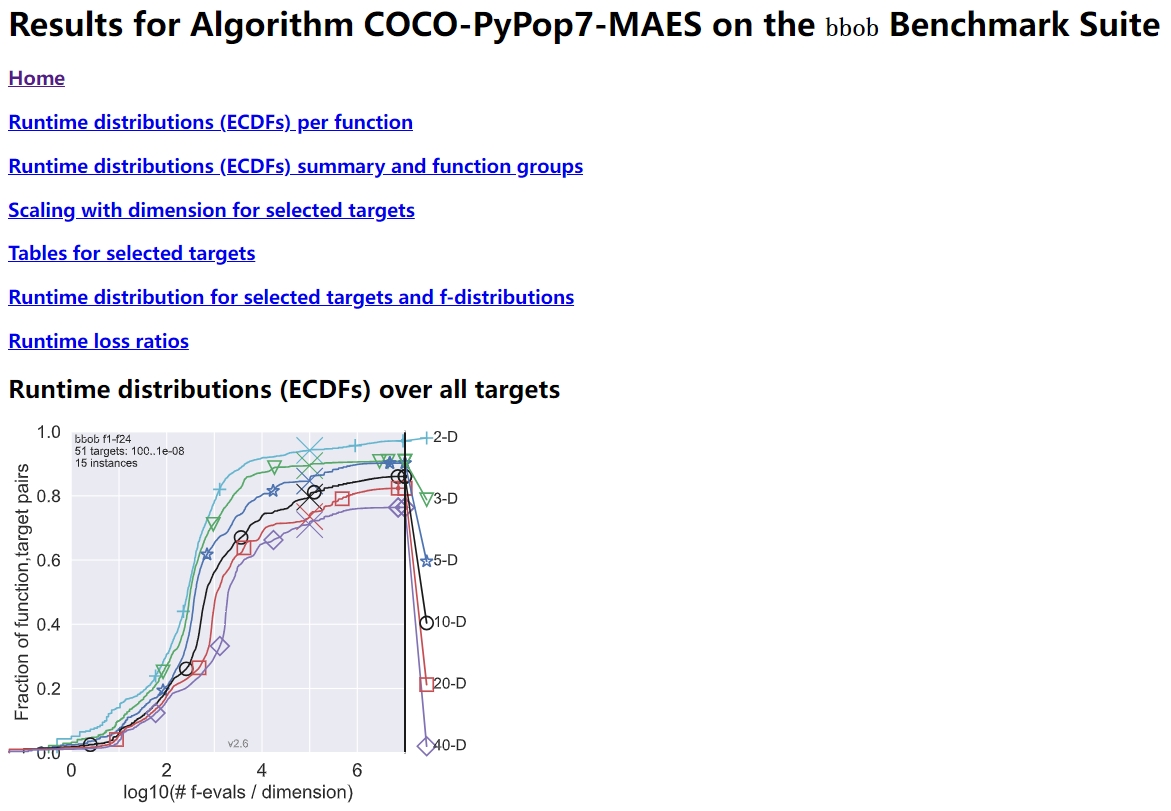
在著名的 NeverGrad 平台上对 BBO 进行基准测试
正如 Facebook AI Research 最近的论文([Meunier et al., 2022, TEVC])所指出的,“现有的黑盒优化研究普遍存在泛化能力低的问题,这是由于在训练和测试不同优化算法时通常选择性地使用问题实例。除其他问题外,这种做法会助长过拟合和产生性能不佳的用户指南。”
在这里,我们选择一个现实世界的优化问题来比较两个基于群体的优化器(PSO vs DE),如下所示
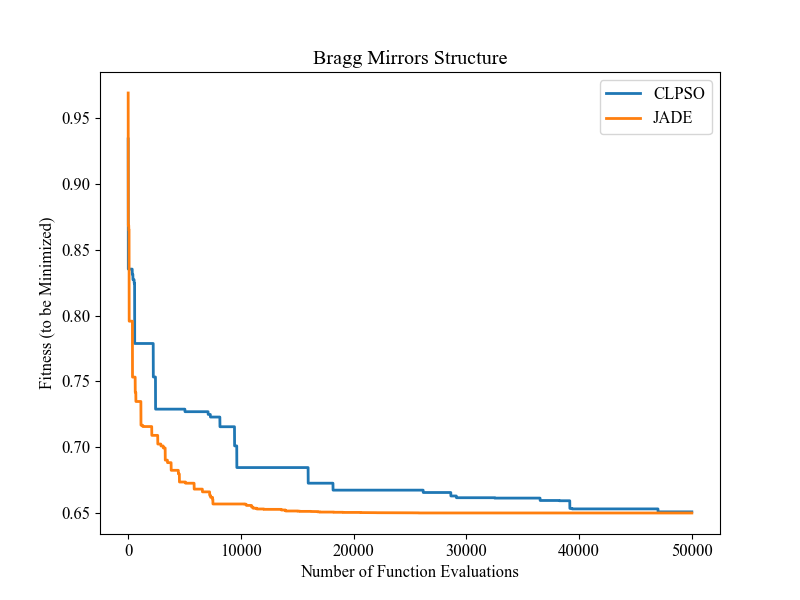
"""Demo that optimizes the Bragg mirrors structure, modeled in the following paper: Bennet, P., Centeno, E., Rapin, J., Teytaud, O. and Moreau, A., 2020. The photonics and ARCoating testbeds in NeverGrad. https://hal.uca.fr/hal-02613161v1 """ import numpy as np import matplotlib.pyplot as plt from nevergrad.functions.photonics.core import Photonics from pypop7.optimizers.pso.clpso import CLPSO # https://pypop.cn/en/latest/pso/clpso.html from pypop7.optimizers.de.jade import JADE # https://pypop.cn/en/latest/de/jade.html if __name__ == '__main__': plt.figure(figsize=(8, 6)) plt.rcParams['font.family'] = 'Times New Roman' plt.rcParams['font.size'] = '12' labels = ['CLPSO', 'JADE'] for i, Opt in enumerate([CLPSO, JADE]): ndim_problem = 10 # dimension of objective function half = int(ndim_problem/2) func = Photonics("bragg", ndim_problem) problem = {'fitness_function': func, 'ndim_problem': ndim_problem, 'lower_boundary': np.hstack((2*np.ones(half), 30*np.ones(half))), 'upper_boundary': np.hstack((3*np.ones(half), 180*np.ones(half)))} options = {'max_function_evaluations': 50000, 'n_individuals': 200, 'is_bound': True, 'seed_rng': 0, 'saving_fitness': 1, 'verbose': 200} solver = Opt(problem, options) results = solver.optimize() res = results['fitness'] plt.plot(res[:, 0], res[:, 1], linewidth=2.0, linestyle='-', label=labels[i]) plt.legend() plt.xlabel('Number of Function Evaluations') plt.ylabel('Fitness (to be Minimized)') plt.title('Bragg Mirrors Structure') plt.savefig('photonics_optimization.png')
最终的图形输出如下所示
更多用法示例
对于这个开源 Python 库中的每个黑盒优化器,我们还在其相应的 API 文档中提供了一个玩具示例,并在其相应的 源代码文件夹中提供了两个测试代码(如果可能)。有关其应用和(他人)赞誉的摘要,请参阅此 html。